Featured Artist Shares Goldbergs Galore

 

王德祥

More About S3

Halloween Theme

Memo re S3

Note that if I build an XYZ skyscraper and an IVM space station side by side, there's no implied scale factor until we start adding the little human construction workers and/or cosmonauts or whatever. The XYZ and IVM scaffoldings each float free of one another in the imagination with no necessary strategy for entangling them. Creating a conversion constant required a designer's touch, as there was no one right answer to mathematically deduce, nor any empirical answer for scientists to uncover.

What's revolutionary about a tetrahedron unit is not its size  relative to the XYZ system, but its shape. The tetrahedron stabilizes the cube and provides an ecosystem in which both have an integer volume, versus only the cube when it's allowed to hog the limelight. The tetrahedron is simpler, topologically, and stronger, structurally. Making it also be unit is a streamlining maneuver that XYZers get awkward about, forgetting to walk their own talk i.e. different axiomatic underpinnings were never verboten nor even defended against. We welcome this example of an alternative paradigm. 

Fuller figured out a way to bring a cube and tetrahedron within 6% of each other by making XYZ edge 1 be a CCP ball radius, and making IVM prime vector (tetra edge) be edge 2, i.e. twice XYZ's. The unifying concept, like the cosmonauts above, is the unit radius CCP ball. Make its radius define the XYZ unit cube  and make its diameter give the edges of the IVM unit tetrahedron. 

 It's a simple story, linking the two scaffolding strategies, the skyscraper and the space station skeletons.

One may also introduce the TetraBook at this point, the one triangular page book, with triangular covers open wide open flat. The page wages back and forth in an arc.

When the page is vertical to the covers, the two right tetrahedrons described, symmetric around this vertical partition, are each equal to that of a cube of edges R, shown in green down below. That's XYZ's unit cube, in the background. In this IVM world (call it Mars), we're modeling the unit cube's volume as a right tetrahedron of all edges D, except for the "hypotenuse" which is even longer.

Tilt the page a little further, either way, and you get a regular tetrahedron and its equal-volumed complement. That's the unit of volume in the IVM system, shown below in blue.

 

High School in the Silicon Forest (Mites Make Rites)

Dissecting Volumes

In Synergetics we closest pack (densely pack) a lot of ideas together. Arthur C. Clarke mentions that in his blurb, on the back of the volume. 

Much of that work is done using tetrahedral wedges or volumes known as modules, sometimes known as "quanta modules" because they quantify discretely. You're welcome to keep it Platonic by not hopping over to quarks right away. 

Fuller is entitled to speculate, but we're likewise free to think more in terms of a game of cellular automata in 3D, using Mite-shaped cells, ala Stephen Wolfram (a new kind of science) and J.H. Conway (a game of life). 

Mites fill space with clones of themselves, possibly by way of other space-filling shapes they build along the way, such as the Cube (3), Coupler (oblate octahedron, volume 1) and the Rhombic Dodecahedron (6).

Bucky himself links his Mite to Donald Coxeter's Regular Polytopes in one of his captions (see below), where Coxeter introduces an orthoscheme of the cube made of half-Mites, or Smites as we might playfully call them (as in "smitten, into semi-Mites").  

Coxeter was into kaleidoscopic reflections, and an orthoscheme, kaleidoscopically reflected, often tends to make a characteristic shape. 

The A module reflects to make a tetrahedron of 24As, 12+ and 12- (left and right), and As are orthoschemes, meaning there's a way to visit all four of its verts by making only 90 degree turns. 

If three right angles meets at a single vertex, it's a trirectangular tetrahedron, but not an orthoscheme.

The B module alone is not an orthoscheme, but an A and B face-bonded together make the 1/48th orthoscheme of the regular octahedron, canonically our volume 4.  1/48 of 4 = 1/12 = 1/24 + 1/24.  A and B are both 1/24.

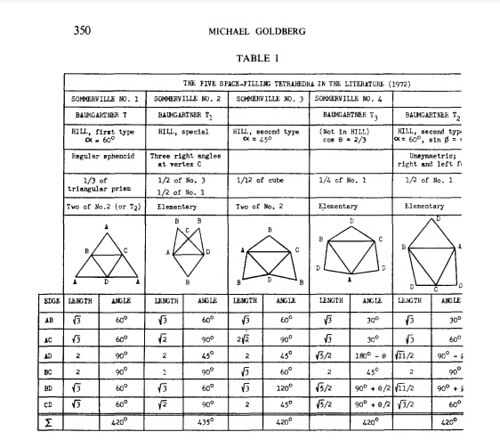
Fig 950.12 Three Self-Packing, Allspace-Filling Irregular Tetrahedra: There are three self-packing irregular tetrahedra that will fill allspace without need of any complementary shape (not even with the need of right- and left-hand versions of themselves). One, the Mite (A), has been proposed by Fuller and described by Coxeter as a tri-rectangular tetrahedron in his book Regular Polytopes, p.71. By joining together two Mites, two varieties of irregular tetrahedra, both called Sytes, can be formed. The tetragonal disphenoid (B), described by Coxeter, is also called the isosceles tetrahedron because it is bounded by four congruent isosceles triangles. The other Syte is formed by joining two Mites by their right-triangle faces (C). It was discovered by Fuller that the Mite has a population of two A quanta modules and one B quanta module (not noted by Coxeter). It is of interest to note that the B quanta module of the Mite may be either right- of left-handed (see the remarks of Arthur L. Loeb). Either of the other two self-packing irregular tetrahedra (Sytes) have a population of four A quanta modules and two B quanta modules, since each Syte consists of two Mites. Since the Mites are the limit case all space-filling system, Mites may have some relationship to quarks. The A quanta module can be folded out of one planar triangle, suggesting that it may be an energy conserver, while the B quanta module can not, suggesting that it may be an energy dissipator. This gives the Mite a population of two energy conservers (A quanta module) and one energy dissipator (B quanta module).

Did Fuller think the Mite and its derivative Sytes (Bite and Rite) where the only self-packing allspace-filling irregular tetrahedrons?  He appears to miss both the half and the quarter Rite, as a self-packing space-fillers.  

In these vZomes by David Koski, the tan triangles are Rite halvers, whereas the two blue planes in the bottom canvas (one of darker shade) slice the Rite into four clone quarters.

The Mite and two Sytes, Rite and Bite, plus the half- and fourth-Rite summarize the five space-filling tetrahedrons known, right before Michael Goldberg introduced a new family.

David Koski has helped us cross-index the Smite's volume in terms of the concentric hierarchy, as also equal to that of the 1/4 Rite, and also to that of each of the 120 E-mod shapes (but bigger) building the rhombic triacontahedron of volume 7.5.

This RT of volume 7.5 (not focused upon in the first two volumes of Synergetics) is sized up by 3/2 (or by a 3rd root of same as a linear scale factor) from the RT of volume 5 (a star of Synergetics 2) which latter is made of 120 T modules (likewise volume 1/24, same as A and B).  

The 7.5 RT pleasingly shares verts with the volume six space-filling RD, another "circuit closer" in our geometric, mnemonic spatial mandala, i.e. the concentric hierarchy.  Four Rites make the Coupler.

Turning Left (Open Source)

This Old House (School of Tomorrow)