Synergetics has taken various twists and turns since the 1970s, when Macmillan came out with the second volume, designed to interleave with the first, and including an index. In that second volume, we got a more complete basis for working with the five-fold symmetric shapes already within the concentric hierarchy, namely the T, E and S modules.
Picking up on that thread, we have since amplified the 120 T-module volume 5 rhombic triacontahedron, of radius just a tad under 1 (0.99948...), to another copy weighing in at 7.5 and sharing a set of tips with the rhombic dodecahedron (RD), of volume 6.
The 120 E-module volume 5+ RT, on the other hand, of radius precisely 1, scales up by Φ (linearly) to give the 15√2 volumed RT, dubbed SuperRT, wherein the Jitterbug Icosahedron of edges 2R, embeds as long diagonals, with a volume of 5√2 Φ2.
The ratio of said Jitterbug Icosahedron to its related larger-volumed cuboctahedron (CO) of equal edges is defined by what David Koski and I are calling the S-factor i.e. CO/Icosa = S/E = (2√2)/Φ2 or (2√2)Φ-2 or about 1.080363.
Starting with any Icosahedron, one application of the S-factor nets the volume of the corresponding CO with same edge lengths, the "Jitterbug" relationship.
Two applications of 1/S-factor (the reciprocal), on the other hand, nets the volume of the corresponding CO with faces flush to the same containing octahedron, the "skew" relationship.
In other words, this smaller-volumed CO and Icosa are skew to one another with overlapping facial regions, as shown in Synergetics 2, Figure 988.00.
For example, the Icosahedron inscribed in the Octahedron of volume 4 has S-factor edges. Two applications of 1/S-factor gives the volume 2.5 CO with edges R, i.e. precisely 1/8th the volume of the 2R 20 volumed JT CO.
CO2.5 * S-factor * S-factor gives the S-factor-edged Icosa inscribed in the volume 4 octa, from whence S-modules are derived.
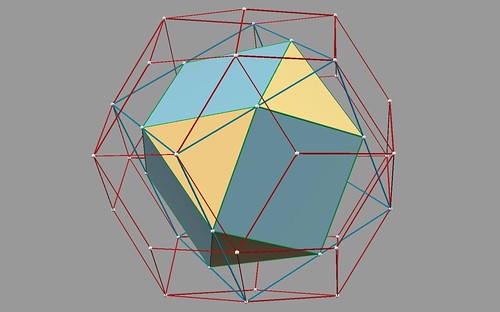
One more application of the S-factor gives the CO shown below, nestled precisely within the RT5+ at the green points.
In contrast, the CO with √2 edges, shown above is precisely 1/3rd the RT5+ volume.
Finally, David realized another relationship: S3, the volumetric version of the Synergetics Constant, ordinarily used to take us from cubic units to tetrahedron units, is also the ratio of SuperRT to the Jitterbug CO. S3 = √(9/8).
Put another way, the RT with long diagonals equal to the Icosahedron from which a CO is developed by Jitterbugging, has a volume S3 times that CO's volume. 20 * S3 = 15√2.
We may also introduce the T-factor as the ratio between the RT5+ and RT5, i.e. the E-modules and T-modules rhombic triacontahedrons. That number is (3√2)/Φ3 or (3√2)Φ-3. The reciprocal of its 3rd root is the linear scale factor 0.99948... (mentioned above) taking us from the E-mods RT to the T-mods RT.