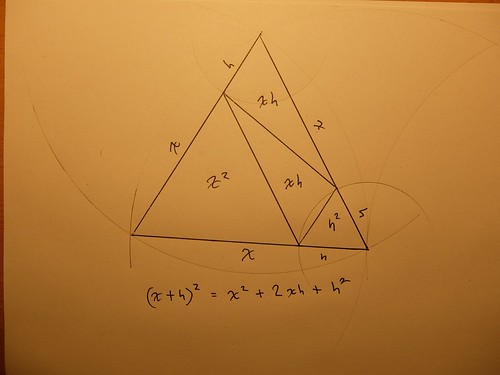I drew this to help Andrius, in Vilnius, visualize an important identity, used in calculus. Going to the next higher power, using a tetrahedron, would be a logical next step.
Princeton is where I ran into Wittgenstein's philosophy, including his Remarks on the Foundations of Mathematics (RFM). When Ludwig wants to "investigate" a math concept, or any concept, he'll often construct "language games" for that purpose.
He does this with intent, as a sketch artist would, to bring forward specific aspects of play that might have been confusing. Language gets to be a tangled mess sometimes. For Wittgenstein, philosophy was a lot about disentangling.
Speaking of disentangling, a theme of my writings has been to separate three meanings of 4D. For example, check out this blog post regarding 4D vs 4D vs 4D.
I'm seeing the 1900s as a period of "shake out" wherein three principal meanings of 4D settled down, each comfortable in its own groove. They're not identical and to confuse them is to become entangled in a web of language.
Coxeter.4D is what we call "extended Euclidean geometry" meaning (x, y) addressing of R x R (a plane), and (x, y, z) addressing of R x R x R (volume), is extended to any number of real number lines or dimensions. Regular Polytopes, by Donald Coxeter, is a major contribution within this lineage.
Einstein.4D introduces time as a space-like dimension in that one's perception of time and motion is a function of one's reference frame relative to others, such that those moving at closer to the speed of light age less quickly than clocks at rest. What's the same across inertial coordinate systems is a space-time interval in which (x, y, z, t) figure in to the computation as four inputs (hence 4D).
Fuller.4D focuses on the primacy of the tetrahedron in the Kantian sense of introducing concepts we cannot shake, such as "enclosure" (container) along with "concavity" (in the cave) and "convexity" (outside the container). We're born with the a priori idea of being "in" something and the tetrahedron is a topologically minimal concept of having an inside.
Donald Coxeter himself was at pains to disambiguate between his extended Euclidean 4D and Einstein's relativity theory's 4D.
We might summarize this difference as "the difference between a tesseract (hypercube) and a time machine", on the understanding this is precisely the difference some science fiction writers may deliberately confuse, as a plot-driving device.
Donald writes, on page 119 of Regular Polytopes:
A first point of contention was around intellectual property, around radomes in particular. The US military honored a US patent in contracting with Fuller's firms for DEW line radomes, situated in Canada.
Donald's son, a Canadian, was hoping to break in to the radar dome business and came up against not owning the relevant patent. Donald went ballistic, thinking such a fundamental geometry of nature would really have to be open source.
Fuller's having patented the octet truss, in addition to the geodesic dome, likely didn't improve matters. Both are found all over the place in naturally occurring physical objects.
The softening in their relationship came with the Montreal Expo '67 geodesic dome, a marvel to behold and huge. Coxeter eventually agreed to let Fuller dedicate Synergetics to him. Synergetics is where Fuller's use of 4D is made clear. Bucky writes:
In computer science we now have the concept of "namespace" which is equivalent to the humanities notion of "context". For example in Python a namespace may be a module, saved in storage as a Python script.
The meaning given to the various names in a script will become evident at runtime. Likewise in the humanities we appreciate that authors have their own unique ways of using certain words, which both borrow from and contribute to shared usage patterns.
Disentangling the meanings of 4D is important to future math, and to one's level of cultural literacy. Our Coffee Shops Network has the LCD reveries that help boost one's understanding of these many nuances and subtleties.
Princeton is where I ran into Wittgenstein's philosophy, including his Remarks on the Foundations of Mathematics (RFM). When Ludwig wants to "investigate" a math concept, or any concept, he'll often construct "language games" for that purpose.
He does this with intent, as a sketch artist would, to bring forward specific aspects of play that might have been confusing. Language gets to be a tangled mess sometimes. For Wittgenstein, philosophy was a lot about disentangling.
Speaking of disentangling, a theme of my writings has been to separate three meanings of 4D. For example, check out this blog post regarding 4D vs 4D vs 4D.
I'm seeing the 1900s as a period of "shake out" wherein three principal meanings of 4D settled down, each comfortable in its own groove. They're not identical and to confuse them is to become entangled in a web of language.
Coxeter.4D is what we call "extended Euclidean geometry" meaning (x, y) addressing of R x R (a plane), and (x, y, z) addressing of R x R x R (volume), is extended to any number of real number lines or dimensions. Regular Polytopes, by Donald Coxeter, is a major contribution within this lineage.
Einstein.4D introduces time as a space-like dimension in that one's perception of time and motion is a function of one's reference frame relative to others, such that those moving at closer to the speed of light age less quickly than clocks at rest. What's the same across inertial coordinate systems is a space-time interval in which (x, y, z, t) figure in to the computation as four inputs (hence 4D).
Fuller.4D focuses on the primacy of the tetrahedron in the Kantian sense of introducing concepts we cannot shake, such as "enclosure" (container) along with "concavity" (in the cave) and "convexity" (outside the container). We're born with the a priori idea of being "in" something and the tetrahedron is a topologically minimal concept of having an inside.
Donald Coxeter himself was at pains to disambiguate between his extended Euclidean 4D and Einstein's relativity theory's 4D.
We might summarize this difference as "the difference between a tesseract (hypercube) and a time machine", on the understanding this is precisely the difference some science fiction writers may deliberately confuse, as a plot-driving device.
Donald writes, on page 119 of Regular Polytopes:
Little, if anything, is gained by representing the fourth Euclidean dimension as time. In fact, this idea, so attractively developed by H.G. Wells in The Time Machine, has led such authors as J. W. Dunne (An Experiment with Time) into a serious misconception of the theory of Relativity. Minkowski's geometry of space-time is not Euclidean, and consequently has no connection with the present investigation. (Dover Publications, 1973)Donald's relationship with Fuller, another spinner of 4D, was somewhat inevitable in hindsight, and might be characterized as "stormy at first, smoothing out into friendship".
A first point of contention was around intellectual property, around radomes in particular. The US military honored a US patent in contracting with Fuller's firms for DEW line radomes, situated in Canada.
Donald's son, a Canadian, was hoping to break in to the radar dome business and came up against not owning the relevant patent. Donald went ballistic, thinking such a fundamental geometry of nature would really have to be open source.
Fuller's having patented the octet truss, in addition to the geodesic dome, likely didn't improve matters. Both are found all over the place in naturally occurring physical objects.
The softening in their relationship came with the Montreal Expo '67 geodesic dome, a marvel to behold and huge. Coxeter eventually agreed to let Fuller dedicate Synergetics to him. Synergetics is where Fuller's use of 4D is made clear. Bucky writes:
527.702 Geometers and "schooled" people speak of length, breadth, and height as constituting a hierarchy of three independent dimensional states --"one-dimensional," "two-dimensional," and "three-dimensional" -- which can be conjoined like building blocks. But length, breadth, and height simply do not exist independently of one another nor independently of all the inherent characteristics of all systems and of all systems' inherent complex of interrelationships with Scenario Universe.
...
Coxeter was also impressed by Fuller's discovery of the cuboctahedron number sequence, 1, 12, 42, 92, 162 and so on, his formula for generating this sequence, and generalizable to other shapes. Clearly Fuller was doing his own thinking to some high degree.527.712 All conceptual consideration is inherently four-dimensional. Thus the primitive is a priori four-dimensional, being always comprised of the four planes of reference of the tetrahedron. There can never be any less than four primitive dimensions. Any one of the stars or point-to-able "points" is a system-ultratunable, tunable, or infratunable but inherently four-dimensional.
In computer science we now have the concept of "namespace" which is equivalent to the humanities notion of "context". For example in Python a namespace may be a module, saved in storage as a Python script.
The meaning given to the various names in a script will become evident at runtime. Likewise in the humanities we appreciate that authors have their own unique ways of using certain words, which both borrow from and contribute to shared usage patterns.
Disentangling the meanings of 4D is important to future math, and to one's level of cultural literacy. Our Coffee Shops Network has the LCD reveries that help boost one's understanding of these many nuances and subtleties.