Self Contained LCDs

The idea of a self-contained LCD stems from having display system and programs in a single unit.

Perhaps a Raspberry Pi or similar GPU-endowed motherboard is tucked away internally within some cabinet, along with the display screen it feeds.

Mount the assembly and plug it in, and it boots into a set repertoire of animations, perhaps with sounds.

Yes, our sign could be little more than a billboard with rotating advertising.  As such, this technology is already out there, next to freeways, at Times Square.

In the CSN context, we use our screens to share reveries, perhaps hypertoons, continuous transformations scanned from a network of scenarios (edges) interconnecting the key frames (nodes).

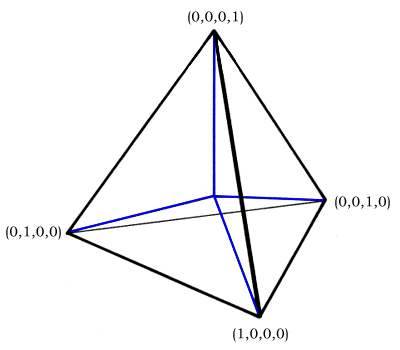
One such hypertoon might feature the assembly and disassembly of well- and lesser-known polyhedrons from phi-scalable tetrahedrons.  The topic is purely abstract, yet precise.

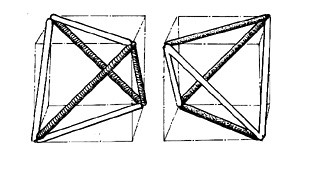
The rhombic triacontahedron (RT) dissects into 120 such modules, left and right handed.

Meanwhile, the regular tetrahedron may be sliced into four quadrants, each of which further subdivides into three pairs of left and right handed versions of the same shape, for a total of 24 modules, differently shaped from the ones above.

Those of us schooled in American transcendentalism have our own vocabulary for these geometric concepts, making it easier for our engineers to communicate with one another.  The RT dissects into E-modules, the regular tetrahedron into A-modules.

The E-shape resized to match the A-shape in volume is the T-module.  You will find all the plane-nets in transcendentalist works but don't expect too much from your literature profs.  Readers in the humanities tend to eschew what appears to be purely technical, even if it's also architectural.  We don't get many polymaths like Hugh Kenner.

Said rhombic triacontahedron, in which two Platonics are inscribed, relates to the rest of the Platonic Five though the Jitterbug Transformation.  The icosahedron and cuboctahedron connect in this way, bridging the two symmetry families (five-fold with four).

When David Koski was through Portland lately, we had a CSN meeting at #CodeCastle, the Sunnyside Methodist Church turned community center.  Some of us had visited PDX Code Guild the night before.

Thanks to our already sharing a lot of the same memes, as a subculture, CSN is well-positioned to move the "coffee shop LCD" to a next level, as an art form.  We've been touring many East-meets-West retail outlets for inspiration.

Will we have some CSN LCDs in Havana, Cuba, in time for SciPy next year?  All the hypertoons I've prototyped in actual computer code have used Python.

Internet Aware LCDs

The display above, by Charles Cossé, runs on a Raspberry Pi.

Connect the Pi to a large display (e.g. HDTV) at your Coffee Shop or Code School, with the right SD card, and you're in business.  Customers enjoy the worldly feel of Internet Awareness.

Other LCDs provide other reveries, such as Hexagonal Awareness.  The LCDs behind the counter show the current menu.  Add a mirror?

Use Raspberry Pis for all of these HDTVs if you wish.

I just backed Th'underGrounds on @Kickstarter https://t.co/gtycZSyvIN

— Kirby Urner (@4DsolutionsPDX) September 30, 2016

Disarm Day 2016

Project Jupyter

Need to share gnu mathematics in an accessible way? Consider @ProjectJupyter notebooks with @ContinuumIO 's Anaconda distro. @planetpython

— Kirby Urner (@4DsolutionsPDX) August 6, 2016

Join our discussion: on the future of math teaching https://t.co/h3uPaPQEU7 @hackingmath @NMSI @NatlPAT @EdWeekTeacher @Raspberry_Pi

— Kirby Urner (@4DsolutionsPDX) August 6, 2016

@ProjectJupyter @ContinuumIO @planetpython https://t.co/qnFe7iufaj

— Kirby Urner (@4DsolutionsPDX) August 6, 2016

https://t.co/mxgxqSqFy5 @ContinuumIO @ProjectJupyter @planetpython #CodeCastle #LearnHex #HP4E

— Kirby Urner (@4DsolutionsPDX) August 6, 2016

Charitable Gaming

:: empowering the network ::

One might think the gamification of philanthropy would have inspired a huge number of businesses by this time.  What better way to be a hero, right?  In a thriving yet studious atmosphere.  Or in your personal workspace (your cubby).  Play, win, donate winnings, self profile.  And repeat.

This blog has been promulgating the business plans in an open source manner, to inspire imitators and create the institutions necessary.  Some argue the churches, Catholic especially, that raise funds through bingo, are already in the game.  Let me point out the differences.

In philanthropy, unlike in Video Poker run by the state, funds are earmarked by the winner, the person having the game-winning skills.  The winnings don't go to some central coffer administered by intermediaries.  Vote your conscience.

Church bingo likewise puts the House (in the sense of Casino) in charge of winnings, forcing players into a selfish role.  Having players contemplate which philanthropies are most worthy inspires doing homework, on the part of the Study Hall as well.

Did I just say "Study Hall"?  What is this, Hogwarts?  I meant "Coffee Shop" of course, in that we have vended goods.  Part of the business plan is to involve the vendors.  They're donating to charity and accounting that under Good Will, per standard bookkeeping practices.

However, the vendors are willing to have players do the work of playing the games, playing to win, and committing the winnings to charitable organizations.  Buy a Voodoo Donut, get a chance at bat.

The vendors may have access to the analytics, for market research purposes, in itself a value.  Some companies may see their advertising budgets as backing these games.  CSN shouldn't have to busy itself with how others choose to keep score.

What games?  Where?

The would-be philanthropic have no idea where to go, to send winnings to refugee camps, in Messy-potamia or wherever.  Hey, sorry for the somewhat crummy pun.  Potamia is a mess these days, I think we'd agree, thanks to the undisciplined use of airspace and sinking groundwater.

Meso means Middle, as in Mesoamerica.  The "meso" became "middle" as in "Middle East", with Potamia always a popular name, used by many places.

However there's no reason a charitable donation has to go half way around the world.  Sometimes those closest to the action have more perspective.  Support projects close to home.  Let people know that you've done so.  Tell the world who you are, by sharing a track record of whom you back.

Rotten Apple Award

And a Rotten Apple award goes to... Mathematics for Elementary School Teachers: A Conceptual Approach. https://t.co/jpJuX2Mm4A #CodeCastle

— Kirby Urner (@4DsolutionsPDX) July 24, 2016

Dumbs it down by withholding #MedalofFreedom mathematics, and just sticks wtih the English stuff. No @BuckyFuller_ https://t.co/CNaUnLQdbx

— Kirby Urner (@4DsolutionsPDX) July 24, 2016

Lots of room for English https://t.co/MdAXK3E5lt but no mention of #MedalofFreedom American heritage. Rotten Apple award. @BuckyFullerInst

— Kirby Urner (@4DsolutionsPDX) July 24, 2016

The Tesseract, the Time Machine and the Tetrahedron

My title above is reminiscent of The Lion, the Witch and the Wardrobe, at least in terms of mentioning three rather disparate things.  That's intentional.  Welcome to Narnia, chuckle.

This campfire story, suitable for children, is about many great minds and how they grappled with their intuitions in different ways, coming up with different games, yet with overlapping memes, such as "dimension" and even "four dimensional".

We associate a Time Machine with H.G. Wells, who also wrote War of the Worlds, but also with Dr. Who I suppose, as what's that Tardis if not an inter-dimensional phone booth?  Milo had his Phantom Tollbooth with similar powers to transport.  If only Gulliver could have had one, to escape the Lilliputians.

However lets talk about Regular Polytopes and their rather gentrified neighborhood, in the sense of rectlinear, properly grided, with its main axial boulevards all meeting at right angles, as many as we need.  The upstanding L, as in perpendicular, rules in this multi-dimensional kingdom, of XYZ on steroids.  Abbott's Flatland helps us get comfortable with our higher dimensional mental powers.

Then Einstein came along with novel propositions about the relativity of simultaneity and therefore causation (as in "who made whom do what"), based on a new kind of dependency, that of one's own coordinate system.  One's point of view determined one's narrative more than we knew, even in physics.  Where you stand depends on where you sit.  Your angle on the action is therefore not "negligible" (nor off the table as a matter for peer review).

Linear independence in the Euclidean sense of XYZ was no longer sufficient, as no one God's Eye  coordinate system (interpreted by His duly appointed minions) could deny the others their physics, and yet these others might nevertheless tell the story in different ways, with different villains and heroes.  Blasphemy!

Logic was not forcing a unique or unitary result, and this seemed threatening to some, especially imperialists. Non-Euclidean geometry seemed subversive (Einstein was Jewish).  However the mathematicians were reassuring:  "we always promised as many rose gardens as you can manage" they said, "given the right fertilizing axioms."

Just the right set of axioms (no pun intended) or game rules, will fuel a fire that burns well, a game that plays.  Some won't become eternal favorites, whereas others may sit on a shelf pending rediscovery by players of matching mindset.  The time capsule effect.  Sleepers awaken.

Finally: the Tetrahedron, and a third chapter in our wandering story.

The primacy of the rectilinear orthodoxy was further called into question.  Why should right angles be so consequential at the end of the day?  They're unavoidable, true, but should they be that definitive?

On Planet Earth, two perpendiculars to the surface are not parallel to one another.  The smaller one is, relative to the planet, the less difference that makes.  But humans had outgrown their flat earth fixations by 1999.  What if the IVM tetrahedron played as well or better with others vis-a-vis the XYZ cube?

Well it turns out we have a choice of flavors.  Either / or is out the window (more a fallacy than a contradiction).  Enjoy them all, and more besides!

Really, I'm just retelling the story of 4D vs. 4D vs. 4D ("three scoops"), which is about three ways in which this 4D meme survived a 20th Century shakeout.  Different generalists commanded each namespace, keeping each coherent enough to avoid flaming out.

The polytope-minded gentry, many of them French, circled their n-dimensional wagons to protect their geometry from what they saw as time-degraded physics, the savage realm of Energy and Entropy.  Euclidean geometry is pre-Newtonian in its aloofness to temporal matters, almost Platonic in its relationships.

The Tetrahedron, meanwhile, wove back and forth somewhere in between, not needing a fourth perpendicular necessarily, for its additional degrees of freedom, yet sympathetic to the timelessness of Euclid and Plato.  The concentric arrangements of Platonics and their progeny was "pre-frequency" until some "frequency" was applied, giving spatiotemporal, special-case meaning.

Yes, this story is a deliberate simplification, as the "dimension" concept is slipperier than a slippery fish.  We have fractional dimensions today, perhaps even irrationally fractional (like pi).  The levels of indeterminacy and interdependency have also increased, with the discovery of quantum entanglement.

But hey, this was enough to get us going, and off to bed, to dream of swimming memes.

Visit your local science museum or library, for more information on the Tesseract (4D hypercube), the Time Machine (piloted by Einstein), and the Tetrahedron (4D in a different sense, just count the arrow tips).

Donate to CSN

[QR-code removed]

As a part of the #CodeCastle cryto-currencies initiative, it makes sense to walk the talk by both sending and receiving bitcoin as an authorized means of upholding one's end of a transaction.

I suggest making only small and non-anonymous donations if using the above QR-code for that. Claim the donation with your own public bitcoin address either just for that purpose or use your general wallet PK.

Do not assume anyone verifies these claims on our end, however the blockchain is public so there will be no doubt about the transaction itself, after some hours, and many donors are well-equipped to authenticate themselves in case their claim is contested.

Do not assume your donation is tax deductible, which is another reason to keep to small amounts. Contributions to a specific nonprofit's fund account would be through a different QR-Code.

The above is to CSN's marketing for CSN's promotion, an account controlled by the CMO (Chief Marketing Officer).  Feel free to earmark though, and to publicize your thinking on CSN in connection with your history of donations.

Come back to this web page for the best QR-code to use.  You can keep a snapshot of what it was at the time to verify your own blockchain transactions.

HP4E Update

 :: link for more discussion ::

A decade ago, I started a media campaign known as HexaPents for Everyone or HP4E.  The Hexapent is another name for a BuckyBall or Fullerene.  The former, Bf, or C60 is the soccer ball topology, however more fullerenes of higher frequency (more hexagons) are conceivable.  There's a C72 and so on.

The gamer community is where HP4E took off, with or without my campaign.  Hexagons have long been a feature of two-dimensional game boards.

Seen from a gods-eye point of view, the player hovers over a plane of hexagons, moving assets around, building or destroying a civilization, as the case may be.

Many gamers realized that, given the Earth is spherical, there was maybe a way to have the hexagonal tiling close back on itself in all circumferential directions.  Those who explored the most deeply discovered the twelve pentagons needed for this closure to occur.

Proposals were floated on the Internet suggesting that Civilization itself, a popular commercial game, adopt this hexapent format.

The HP4E memeplex likewise has become a part of various global models of a more scientific bent, as carving the Earth into tetrahedral wedges, of which the hexagons and pentagons are composed, makes for a cellular data structure subject to various algorithmic techniques.

The mapping giants, Google Earth and ESRI, have offered somewhat muted support for hexapent displays.

The commercial mapping world is still fixated on spherical trapezoids, which become more square towards the equator.  These are no more equi-angular or equi-area than the hexagons and pentagons, but lat / long is what we're used to.

Fortunately, given the power of computer algorithms, it's not an either / or relationship and the hexapent matrix has a bright future even in the commercial sector (my prediction).

Finally, I've long been waiting for the crystal ball, also known as the "disco ball", to come out in hexapent form.

With CAD and laser cutters, getting the mirrors to be hexagons and pentagons, or even triangles, is not impossible.  A new brand could establish itself almost overnight.  I scan the Web for adverts.

NeuroToon

Is is still called anthropomorphism, even when they're not human?

Future Math

I drew this to help Andrius, in Vilnius, visualize an important identity, used in calculus.  Going to the next higher power, using a tetrahedron, would be a logical next step.

Princeton is where I ran into Wittgenstein's philosophy, including his Remarks on the Foundations of Mathematics (RFM).  When Ludwig wants to "investigate" a math concept, or any concept, he'll often construct "language games" for that purpose.

He does this with intent, as a sketch artist would, to bring forward specific aspects of play that might have been confusing.  Language gets to be a tangled mess sometimes.  For Wittgenstein, philosophy was a lot about disentangling.

Speaking of disentangling, a theme of my writings has been to separate three meanings of 4D.  For example, check out this blog post regarding 4D vs 4D vs 4D.

I'm seeing the 1900s as a period of "shake out" wherein three principal meanings of 4D settled down, each comfortable in its own groove.  They're not identical and to confuse them is to become entangled in a web of language.

Coxeter.4D is what we call "extended Euclidean geometry" meaning (x, y) addressing of R x R (a plane), and (x, y, z) addressing of R x R x R (volume), is extended to any number of real number lines or dimensions.  Regular Polytopes, by Donald Coxeter, is a major contribution within this lineage.

Einstein.4D introduces time as a space-like dimension in that one's perception of time and motion is a function of one's reference frame relative to others, such that those moving at closer to the speed of light age less quickly than clocks at rest.  What's the same across inertial coordinate systems is a space-time interval in which (x, y, z, t) figure in to the computation as four inputs (hence 4D).

Fuller.4D focuses on the primacy of the tetrahedron in the Kantian sense of introducing concepts we cannot shake, such as "enclosure" (container) along with "concavity" (in the cave) and "convexity" (outside the container).  We're born with the a priori idea of being "in" something and the tetrahedron is a topologically minimal concept of having an inside.

Donald Coxeter himself was at pains to disambiguate between his extended Euclidean 4D and Einstein's relativity theory's 4D.

We might summarize this difference as "the difference between a tesseract (hypercube) and a time machine", on the understanding this is precisely the difference some science fiction writers may deliberately confuse, as a plot-driving device.

Donald writes, on page 119 of Regular Polytopes:

Little, if anything, is gained by representing the fourth Euclidean dimension as time. In fact, this idea, so attractively developed by H.G. Wells in The Time Machine, has led such authors as J. W. Dunne (An Experiment with Time) into a serious misconception of the theory of Relativity. Minkowski's geometry of space-time is not Euclidean, and consequently has no connection with the present investigation.  (Dover Publications, 1973)

Donald's relationship with Fuller, another spinner of 4D, was somewhat inevitable in hindsight, and might be characterized as "stormy at first, smoothing out into friendship".

A first point of contention was around intellectual property, around radomes in particular.  The US military honored a US patent in contracting with Fuller's firms for DEW line radomes, situated in Canada.

Donald's son, a Canadian, was hoping to break in to the radar dome business and came up against not owning the relevant patent.  Donald went ballistic, thinking such a fundamental geometry of nature would really have to be open source.

Fuller's having patented the octet truss, in addition to the geodesic dome, likely didn't improve matters.  Both are found all over the place in naturally occurring physical objects.

The softening in their relationship came with the Montreal Expo '67 geodesic dome, a marvel to behold and huge.  Coxeter eventually agreed to let Fuller dedicate Synergetics to him.  Synergetics is where Fuller's use of 4D is made clear.  Bucky writes:

527.702 Geometers and "schooled" people speak of length, breadth, and height as constituting a hierarchy of three independent dimensional states --"one-dimensional," "two-dimensional," and "three-dimensional" -- which can be conjoined like building blocks. But length, breadth, and height simply do not exist independently of one another nor independently of all the inherent characteristics of all systems and of all systems' inherent complex of interrelationships with Scenario Universe.

...

527.712 All conceptual consideration is inherently four-dimensional. Thus the primitive is a priori four-dimensional, being always comprised of the four planes of reference of the tetrahedron. There can never be any less than four primitive dimensions. Any one of the stars or point-to-able "points" is a system-ultratunable, tunable, or infratunable but inherently four-dimensional.

Coxeter was also impressed by Fuller's discovery of the cuboctahedron number sequence, 1, 12, 42, 92, 162 and so on, his formula for generating this sequence, and generalizable to other shapes.  Clearly Fuller was doing his own thinking to some high degree.

In computer science we now have the concept of "namespace" which is equivalent to the humanities notion of "context".  For example in Python a namespace may be a module, saved in storage as a Python script.

The meaning given to the various names in a script will become evident at runtime.  Likewise in the humanities we appreciate that authors have their own unique ways of using certain words, which both borrow from and contribute to shared usage patterns.

Disentangling the meanings of 4D is important to future math, and to one's level of cultural literacy.  Our Coffee Shops Network has the LCD reveries that help boost one's understanding of these many nuances and subtleties.

by Hollister (Hop) David
(with attribution to me)

Business Model in Bitcoin

Although suggestive of Bitcoin in particular, the CSN model operates with any currency, crypto or not.

Customers of the Coffee Shop buy vended goods (e.g. snacks + coffee), with a percentage of the sale price committing to a Service Pool, which the vendor tallies as after-profit charitable contributions or Good Will (a legit line item in most charts of accounts).

Customers have the option to multiply winnings, drawing from the Service Pool, with said winnings committed to the service organization (or Cause) of the player's choice.  The shop is doubling as a center for engaging in philanthropic behaviors.

Not shown in this diagram:  the customer's option to add victories (donations) to a profile (chronology).  What better way to advertise one's values?  Show a track record of philanthropic giving, thanks to CSN infrastructure.

Other posts spell out more details as to how pooled Good Will might aggregate faster than payout in some phases, slower in others.  Imagine aggregate player ability as a variable, like collective IQ.  Would we want to re-normalize the games i.e. make them harder or easier, to control payout?   Changing the rules punishes those specializing in mastering a given sport.  Changing the payout is easier, though one may argue devaluing a game's relative payout is a change in the rules.

You'll likely notice that Casinos which do feature skill aspects to some games, face similar queries, which is why CSN is sometimes branded a casino chain, even with proceeds going to worthy causes other than self in most transactions, and not "the house" either, as the customers get to earmark and profile accordingly.

CSN shops (nodes) do have some control over the menu however i.e. the range of worthy causes to which winners may commit their winnings.  Customers are free to shop around and/or play from home so shop constraints are not that onerous, merely reflective of a shop's own profile (a way of branding).

4D Meme

Fig 1: three number lines

If three number lines are place tip-to-tip in a zig-zag (non-coplanar), a half-tetrahedron (pink) will be defined, complemented by the other half (black).

Fig 2: three-vector zig-zags
from Fig 110A of Synergetics

Picture the three number lines (each made of two rays), starting as line segments, then growing or subdividing without limit.

These same three number lines, made mutually orthogonal, define the origin (0,0,0) in XYZ.  These number lines likewise extend without limit to define volume or all-space.

Given six number-line edges define volume (3 + 3), we may say space is 3D.  The pink zig-zag of three segments might even feature two right angular turns.  The set {(1,0,0),(0,1,0),(0,0,1)} is cast as the basis set for spanning this space.  Every point is reachable by (x i, y j, z k) where x,y,z are Real numbers.

Alternatively, we may highlight the four vertexes and faces of the full tetrahedron and define res extensa as inherently 4D (self-evident fourness), with quadrays (caltrop coordinates) emanating in four directions from origin (0,0,0,0) and spanning space in linear combinations, no negating operation required.

 

Fig 3: Q-rays

In Fig. 1, R³ is shown as a "4D" tetrahedron (pink and black). In Fig. 3, the four basis vectors (1,0,0,0), (0,1,0,0), (0,0,1,0), (0,0,0,1) with scalar multiplication by non-negative numbers are sufficient to span R³ through linear combinations.

Although we may consider space 4D, given the iconic stature of the tetrahedron, upon subdividing the edges to show growth by subdivision, we obtain a 3rd power sequence relative to the frequency of the edges.  3rd powering is likewise illustrated with a tetrahedron.

Fig 4
Fig. 4: 3rd Powering
from Fig. 990.01 in Synergetics

In the shoptalk of XYZ, we say R³ is 3D.  However, the all-positive basis vectors remain helpless to reach 7/8ths of space without the operation of negation -- flipping 180 degrees -- an operation provided by scalar multiplication in conventional linear algebra, and providing the additional -i, -j, -k of the familiar "jack" pattern.

In the shoptalk of Synergetics, we say the IVM is 4D, given the self-evident fourness of the tetrahedron, yet without denying 1:2:3 power aspect of linear : areal : volumetric growth.  The four all-positive basis vectors do not require the flipping operation of negation (by definition rotation) to span all-space, only vector scaling and vector addition.

Quadray Coordinates

Traditional XYZ vectors:

A lot of what I'm writing here applies to teaching (x,y,z) vectors of the ordinary kind. 

Given six vectors: {(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1), (0,0,-1)} we're able to reach any point in RxRxR (volume) as addressed by (x,y,z) using:

(A)  the operation of addition (V + V -> V, V a vector)
(B)  the operation of scaling (s * V -> V, s a scalar)

(A) is the familiar tip-to-tail linking of vectors, whereas (B) allows for "grow" (extend) and "shrink" (shorten), as well as "reversal" (180 degree flip).

One could say {(1,0,0),(0,1,0),(0,0,1)} with (A) and (B) is sufficient to span R3 (RxRxR) given simply negation, which we could call "multiplication by -1" i.e. (-1) * (1,0,0) = (-1,0,0).

Without flipping 180 degrees, and given only positive scalar multiplication, the original three basis vectors only span one octant of XYZ space: the all-positive octant.

If negation is allowed, then one more vector: -(x+y+z) would be sufficient to give an all-octant spanning set (we would have the caltrop again, albeit with different angles).

We may think of XYZ vectors as a "jack" of six spokes (six rays) emanating from the origin.  We can put a cube around the origin (0,0,0) and show the six rays poking through the face centers of said cube.  In this scenario, all vectors tail-originate i.e. they have one end at the origin.

When we add vectors, we may place them "tip to tail" which conceptually involves translating one vector such that its tail is at the tip of the other, but the sum of the two is once again tail-originating.

If we wish to express a line segment that does not have an end at (0,0,0), we express it with two end-point vectors.  That would give us the line segments needed to build any wire-frame polyhedron.

Quadrays:

Quadrays likewise span R3 but start with only four rays instead of the six in XYZ (including the three 180 degree flipped basis vectors, for reaching all eight octants with only positive number scaling).

These four basis vectors may be expressed as: {(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)} and span all of R3 using addition and scaling, without needing the "flipping" operation.

All points are reached as a linear combination of these basis quadrays, each scaled in the direction it's already pointing.

Again, instead of a "jack" of six vectors, we have a "caltrop" of four.

We may draw them from the origin (0,0,0,0) to the four corners of a regular tetrahedron.

XYZ & Quadrays Together:

How shall we orient the regular Quadray tetrahedron vis-a-vis an XYZ cube? 

The canonical relationship I'm using puts (1,0,0,0) at the corner of a cube in the first XYZ octant, the all positives octant.  The corresponding tetrahedron has corners in octants (+,+,+), (-,-,+), (-,+,-) and (+,-,-).

Picture two line segments, one above the XY plane, the other below it, at 90 degrees to one another (but not intersecting).  Either edge may be considered a "spine" with "wings tips" at the other edge's end points.

See Figure:

The cube is upside down i.e. the XYZ positive octant is where we would usually put (1,0,0,0)). Quadrays are shown in blue.

However the size of this cube is "all face diagonals = 2" which means the so-called "basis vectors" (four of them) are not "unit" in length.  What's more important, for a starting place, is that the edges of this canonical tetrahedron have all edges 2.  We might call this the "basis tetrahedron" (or "home base").

What is this cube of face diagonals 2 relative to in terms of sphere packing?  Think of three unit radius balls packed tightly into a triangle with a fourth ball nested on the valley these three form, on either side of the triangle.

That makes a tetrahedron of balls with edges going from ball-center to ball-center.  Each edge has length 2R (twice the radius of each ball) or D (the diameter of each ball).

Figures:
http://www.rwgrayprojects.com/synergetics/s09/figs/f86161.html
http://www.rwgrayprojects.com/synergetics/s04/figs/f1105.html

Vector Addition:

How do we add two vectors in XYZ?  Easy:  we simply sum their respective (x,y,z) coordinates.  If v0 = (x0,y0,z0) and v1 = (x1,y1,z1) then v0 + v1 = (x0+x1, y0+y1, z0+z1).

Concrete example: (1,2,3) + (-1,-2,-3) = (0,0,0).

Negating the first set of basis quadrays to get a second set, i.e. the remaining four corners of the 8-vertex cube, may be done with scalar multiplication, however the second set of quadrays defining the "inverse tetrahedron" (the dual of the first, same volume) does not need to introduce any negative numbers. 

The first set was already sufficient to map (span, address) space, so our 4-tuples are free to remain entirely non-negative in their final (reduced, normalized, canonical) expression.

- (1,0,0,0) = (-1,0,0,0) = (0,1,1,1)  (i.e. 180 degree flipped)
i.e. a vector pointing oppositely.

The four "negative" quadrays, pointing at 180 degree to the first four would then be:

{(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.

The two sets together define the eight vertexes of a cube.

Note the four pairs of inverse vectors always sum to the identity vector e.

(1,0,0,0) + (0,1,1,1) = (1,1,1,1) = (0,0,0,0) = e

(0,1,0,0) + (1,0,1,1) = (1,1,1,1) = (0,0,0,0) = e

and so on.  XYZ is the same way:  v + (-v) = e = (0,0,0).

We see that the operation of vector addition with quadrays involves a two step algorithm:

Step 1: add corresponding elements in each 4-tuple, then

Step 2: normalize to the canonical representation using an identity bringing the minimum element (which may be a negative number) to zero. 

Subtracting two quadrays is syntactic sugar for adding the inverse i.e. q0 - q1 = q0 + (-q1).  A negated quadray may always be expressed in canonical (non-negative element) form.

Example:

(1,1,2,0) - (3,1,1,0) = (1,1,2,0) + (-3, -1, -1, 0) = (-2, 0, 1, 0) = (-2, 0, 1, 0) + (2,2,2,2) = (0, 2, 3, 2)

We might also do it this way: (1,1,2,0) - (3,1,1,0) = (1,1,2,0) + (0, 2, 2, 3) = (1, 3, 4, 3) = (0, 2, 3, 2)

Note that (1,3,4,3) is not canonical form either, as we still need to apply Step 2:  subtract the minimum element from all four i.e. (1,3,4,3) - (1,1,1,1) = (0,2,3,2).

We're done when one or more elements is 0 and the others are non-negative.

A secondary canonical form, used interimly in some algorithms, allows negative numbers but requires the four coordinates add to zero.  (2,0,1,1) becomes (1,-1,0,0) by adding (-1, -1, -1, -1).

Any (a, a, a, a) = (0, 0, 0, 0) = e because the four vectors (a,0,0,0) + (0,a,0,0) + (0,0,a,0) + (0,0,0,a) cancel one another out and sum to the origin.  

XYZ is like this too: adding all six spokes of "the jack" nets to the zero sum vector i.e. e (identity element for vector addition).

Conclusions:

What's been defined above so far is sufficient to provide:

(i) a distance formula (length formula) for any quadray vector, such that |v| -> Number were v is a quadray (this is well developed in other writings, as well as in computer code).

(ii) a conversion algorithm whereby any (x,y,z) coordinate may be expressed as a unique quadray in canonical form, and vice versa:  every quadray may be expressed in (x,y,z) coordinates (also implemented).

One property of Quadrays that's interesting then, is they're isomorphic to XYZ.

Consider that spherical coordinates (r, theta, alpha) are also a useful expression of all the same points  addressed by (x,y,z).  Isomorphism is a feature, not an unnecessary redundancy.  Sometimes computing in an alternative representation is more convenient and/or generative of new insights.

Quadray coordinates, like spherical coordinates, give another unique address for the same point in space. They could be introduced in conjunction with spherical coordinates as an alternative representation.

Another property of quadrays is their ability to sum, using only positive integer 4-tuples, to give the vertexes needed for a canonical set of concentric polyhedrons, starting with the basis tetrahedron of edges 2R and volume one.

Volume one?  That's not conventional in XYZ thinking either, but we have a logical foundation for using this alternative model, with a triangular analog. The implications of this alternative logic are worth exploring.

If we adopt the unit-tet model then we likewise get whole number volumes for (volumes in parens):

• the canonical quadray cube described above (3) 
• its dual octahedron where edges cross (4) 
• their combination as a rhombic dodecahedron (6) and 
• the 12-balls-around-1 cuboctahedron that characterizes any ball in the CCP lattice (20). 

For example the corners of the latter cuboctahedron are simply the 12 points:

{(2, 1, 1, 0), (2, 1, 0, 1), (2, 1, 1, 0), (2, 1, 0, 1), (2, 0, 1, 1), (2, 0, 1, 1),
 (1, 2, 1, 0), (1, 2, 0, 1), (1, 1, 2, 0), (1, 1, 0, 2), (1, 0, 2, 1), (1, 0, 1, 2),
 (1, 2, 1, 0), (1, 2, 0, 1), (1, 1, 2, 0), (1, 1, 0, 2), (1, 0, 2, 1), (1, 0, 1, 2),
 (0, 2, 1, 1), (0, 2, 1, 1), (0, 1, 2, 1), (0, 1, 1, 2), (0, 1, 2, 1), (0, 1, 1, 2)}

i.e. all combinations of {2,1,1,0}. 

Restricting quadray addition to a pool of only these, disallowing any scaling, gives the vertexes of the CPP (= FCC), the dense-packing (~74% ) of unit-radius balls, a "home base" in crystallography.

Also true, though not proved here:  any tetrahedron defined by four CCP vertexes has a whole number volume relative to our canonical reference tetrahedron of volume one.

For further reading:
The Quadray Papers
Posting to mathfuture (April 25, 2016)

Nonsense Numbers

:: divergent numbers ::

When I visited the Earlham College campus in Indiana some months ago, I was privileged to address the Philosophy Club, somewhat extra-curricular yet affiliated with the philosophy department.  I briefly went over a discussion we'd been having on math-teach (The Math Forum / Drexel) regarding the following:

We all know about Cantor's work showing N and R belong to different orders of infinity.  We can make elements of N (1,2,3...) pair with all the rationals Q by a well defined process, but we can show that no plodding method forward will map all of R with members of N.

But is N itself "numerable" in the Cantorian sense?  Consider what I call "mirror pi" which is just the digits of pi-to-the right "reflected in the mirror"

3.14159... -> ...951413

The 3-dots (...) signify that the digits go on forever per known algorithms, in both cases.  On the left, we say we're converging to some R.  On the right, I'd say we're "diverging" to a specific element in N, which likewise has infinite digits. 

What it takes to be "specific" is simply an algorithm.  The notion of "convergence" as getting smaller and smaller (closer and closer) is distinct from the concept of "specificity".  Think of serial numbers without ordering (no > or <, only == and !=).

Or we could simply write pi like this:  314159... with the understanding that we'll never make use of a decimal point.  We'll just keep writing a longer and longer string of numbers.

One may imagine some quantity getting bigger and bigger, but think of it instead as writing the unique (but infinite) serial number for some grain of sand on the beach, a member of R (right?), and in this case also a member of N (a positive integer).

I think you'll find a lot of die-hards wanna keep numbers like 314159... out of N, because leaving them in messes with N and R having different Aleph numbers.

We also want to keep the idea of "unique infinity" in some way i.e. if all these "infinite serial numbers" are both truly infinitely big (the reciprocal of infinitely small) and yet are each "specific to one element in the set R" (true in case of pi in R, but argued about. with respect to mirror-pi).

In that case, if each is unique, then may we write:  314159.... (pi's digits) > 161803... (phi's digits)?  What about 999123... > 55555... > 1239... ?  Some will say this expression is meaningless, because these are meaningless strings masquerading as signifying numbers.

Would making the rule for extending them help at all?

The use of the inequality sign above violates our sense of a "unique infinity" (or do we have that sense?).  The idea that 999... (always 9s) has a "permanent head start in its most significant digit" over 333...  (always 3s) seems more of an argument that < and > should go away with "numbers" written like this.

Ordering is not defined, merely equality and inequality?  If that's accepted, then these are not members of N as N has a well-defined notion of ordering right?  There's never doubt about which element is greater, given two elements.  Is that so by theorem or by axiom I wonder?

I propose we name this "set of infinite serial numbers" (which have many properties in common with members of N) the "nonsense numbers" which "diverge to a unique significand" (that object which the number symbolizes -- we're taught to think some name->object model applies when it comes to ordinary infinitely digits pi in any case, a standard part of the mental baggage).

It will be difficult to distinguish Nonsense Numbers from actual members of N however i.e. how would we know for sure, if these are actually distinct sets.  In which set should we put 22222.... (always 2). 

Given N is defined to be infinite, it follows that it *must* have room for such numbers with an infinite number of digits (if not, N is finite, a contradiction), so that really argues for the Nonsense Numbers being a subset of N. 

Perhaps that's how we should teach them then? 

"N is for Nonsense Numbers" (otherwise known as Natural Numbers,only some of which have finite digits).

[first draft posted to mathfuture earlier same day]

For further reading:

MathFuture ›

a question about infinity / countability

Base Camp Meets Coffee Shop

I find it both anomalous and fitting that my "math is an outdoor sport" scouting meme, and my Coffee Shops Network meme, are floating together.

The scouting meme connects to the more discipline experience of life on base, training, a boot camp, with the coffee shop a place to relax and unwind, off base, a safe retreat.

The two institutions balance one another.  Student union.  Back stage (off script).

The reveries on the LCDs help with studying, with some reveries doubling as thinly veiled PR for whatever superstar course.  Come to space camp or whatever.  Remember we have winner philanthropists in the room.  Even if they don't sign up themselves, they might sponsor.

If you're looking for opportunities, just watching these screens will give you ideas sometimes.

However there's no need to be too impulsive.

A good boot camp is surrounded with a gradient, different levels of commitment.  Help students feel their way forward.  Road maps:  also a good idea.  Take the Introduction to Programming course, find out which "full stack" or "tool chain" might best fit your dreams.

I'm using "code school" and "boot camp" almost interchangeably, but then injecting more from the cooking and camping arenas, more farming.  The Internet of Things does not always mean tiny things.

Cooking in an industrial kitchen teaches about concurrency (kept promises trigger what to do next), as does theater whereas coding for exceptions handles promises not kept.  Things happen.

As I was mentioning on mathfuture earlier this morning, we want a Tractor class in part because we may be using a real tractor later that same day, or in a next work/study stint.

Software engineering, sensors, tracking inventory, weighing costs (trade-offs):  this is systems analysis and agile, all rolled into one.

World Game Meetup

I joined a bunch of Meetups on Meetup.com to ring in the new year, and in so doing found out about the Portland World Game meetup.

The group was staging a "positive protest" (not against anything) that very day, New Year's Day, in the South Park blocks.

I was on a tight schedule so only managed a few shots during the setup phase.  I got into a conversation with a guy, only four months in Portland, about how prolific Fuller was (the genius behind the World Game meme).  Operating Manual for Spaceship Earth was one of his more influential titles.

I pointed to the nearby Arlington Club as where Ed and June Applewhite had stayed, when visiting Portland in the 1990s.  Ed was Fuller's chief collaborator on the two Synergetics volumes.  He wrote Cosmic Fishing to chronicle that experience.